On MDPI, a new paper from SSEL on the Univariate Theory of Functional Connections
Univariate Theory of Functional Connections Applied to Component Constraints
Daniele Mortari and Roberto Furfaro have recently published a new paper on MDPI - Mathematical and Computational Applications.
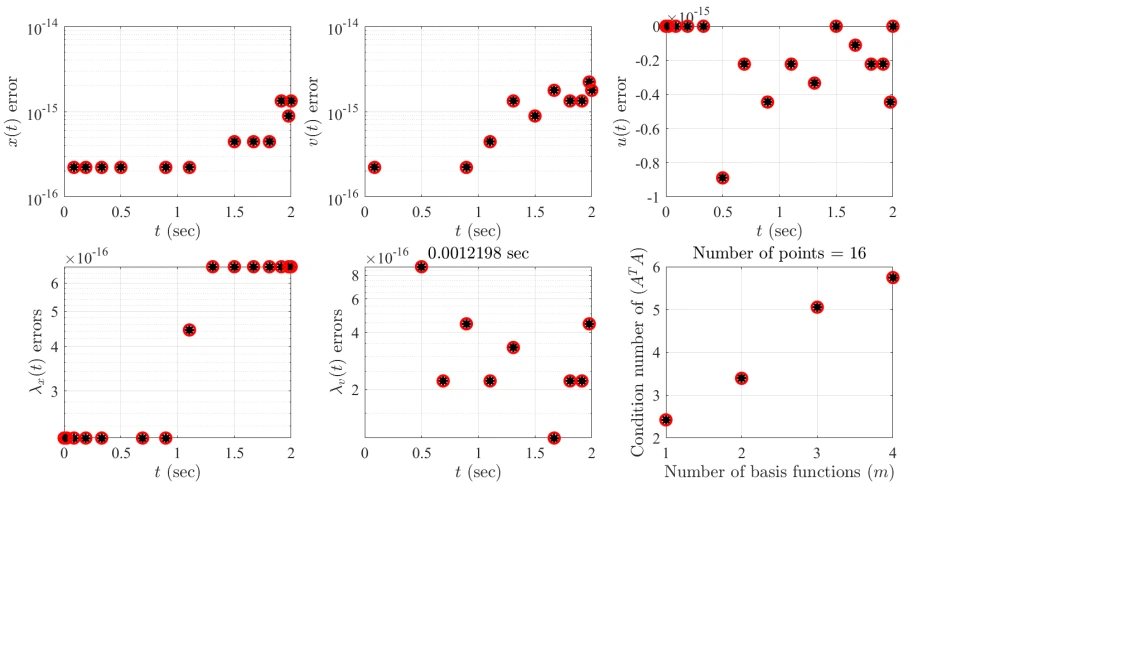
This work presents a methodology to derive analytical functionals, with embedded linear constraints among the components of a vector (e.g., coordinates) that is a function a single variable (e.g., time). This work prepares the background necessary for the indirect solution of optimal control problems via the application of the Pontryagin Maximum Principle. The methodology presented is part of the univariate Theory of Functional Connections that has been developed to solve constrained optimization problems. To increase the clarity and practical aspects of the proposed method, the work is mostly presented via examples of applications rather than via rigorous mathematical definitions and proofs.
You can read it on MDPI:
https://www.mdpi.com/2297-8747/26/1/9/htm
or ResearchGate:

