Extreme Theory of Functional Connections

Extreme Theory of Functional Connections: A Physics-Informed Neural Network Method for Solving Parametric Differential Equations

Enrico Schiassi, Carl Leake, Mario De Florio, Hunter Johnston, Roberto Furfaro, Daniele Mortari

In this work, we present a novel, accurate, and robust physics-informed neural network method for solving problems involving parametric differential equations (DEs) called the Extreme Theory of Functional Connections, or X-TFC. The proposed method is a synergy of two recently developed frameworks for solving problems involving parametric DEs, the Theory of Functional Connections TFC, developed by Mortari, and the Physics-Informed Neural Networks PINN methods. Although this work focuses on the solution of exact problems involving parametric DEs (i.e. problems where the modeling errors negligible) with known parameters, X-TFC can also be used for data-driven solutions and data-driven parameters discovery of parametric DEs. In the proposed method, the latent solution of the parametric DEsis approximated by a TFC constrained expression that uses a Neural Network (NN) as the free-function. This approximate solution form always analytically satisfies the constraints of the DE, while maintaining a NN with unconstrained parameters, like the Deep-TFC method by Leake et al. X-TFC differs from PINN and Deep-TFC; whereas PINN and Deep-TFC use a deep-NN, X-TFC uses a single-layer NN, or more precisely, an Extreme Learning Machine (ELM). This choice is based on the properties of the ELM algorithm developed by Huang et al. In order to numerically validate the method, it was tested over a range of problems including the approximation of solutions to linear and non-linear ordinary DEs (ODEs), systems of ODEs (SODEs), and partial DEs (PDEs). The results show that X-TFC achieves high accuracy with low computational time and thus it is comparable with the other state-of-the-art methods.

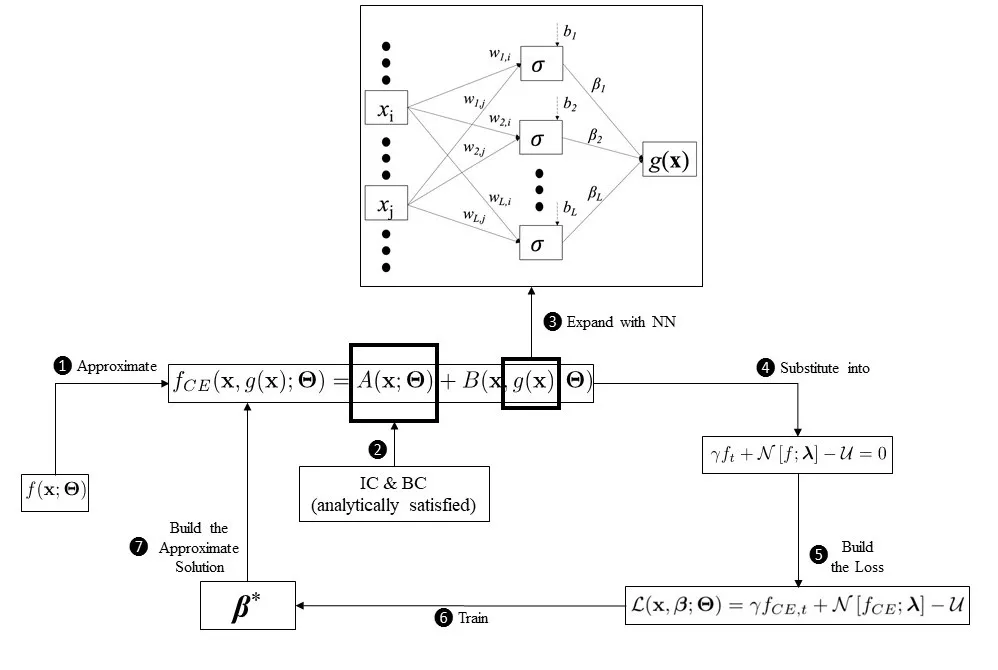
The Figure below shows the schematic of the physics-informed X-TFC framework to solve exact forward problems involving parametric DEs.

Publications

• E. Schiassi, R. Furfaro, C. Leake, M. De Florio, H. Johnston, D. Mortari, Extreme Theory of Functional Connections: A Fast Physics-Informed Neural Network Method for Solving Ordinary and Partial Differential Equations, Neurocomputing (2021). DOI: https://doi.org/10.1016/j.neucom.2021.06.015
• Schiassi, E., Leake, C., De Florio, M., Johnston, H., Furfaro, R., & Mortari, D. (2020). Extreme Theory of Functional Connections: A Physics-Informed Neural Network Method for Solving Parametric Differential Equations. arXiv :2005.10632. PDF